Axis of Symmetry of a Parabola

‍

Symmetry shows the balanced and proportional relationship between different parts of an object, shape, or function. It's an important concept to grasp in geometry, algebra, and calculus. In a quadratic function, the axis of symmetry is the line that divides the parabola into two halves. Let’s explore this further below.

‍

In this lesson, you’ll learn:

• What is an axis of symmetry

• The axis of symmetry formula

• How to find the axis of symmetry of a parabola

‍

‍

What is the Axis of Symmetry?

‍

The axis of symmetry of a parabola is a vertical line that divides the parabola into two equal, mirror-image halves. 

‍

For a quadratic equation in standard form: y = ax² + bx +c

‍

The axis of symmetry formula is: x= -b/2a

‍

This line passes through the vertex and helps identify the parabola's highest or lowest point, depending on whether it opens upward or downward.

‍

‍

Find the Axis of Symmetry of a Parabola

‍

1. Identify coefficients from the quadratic equation.

‍

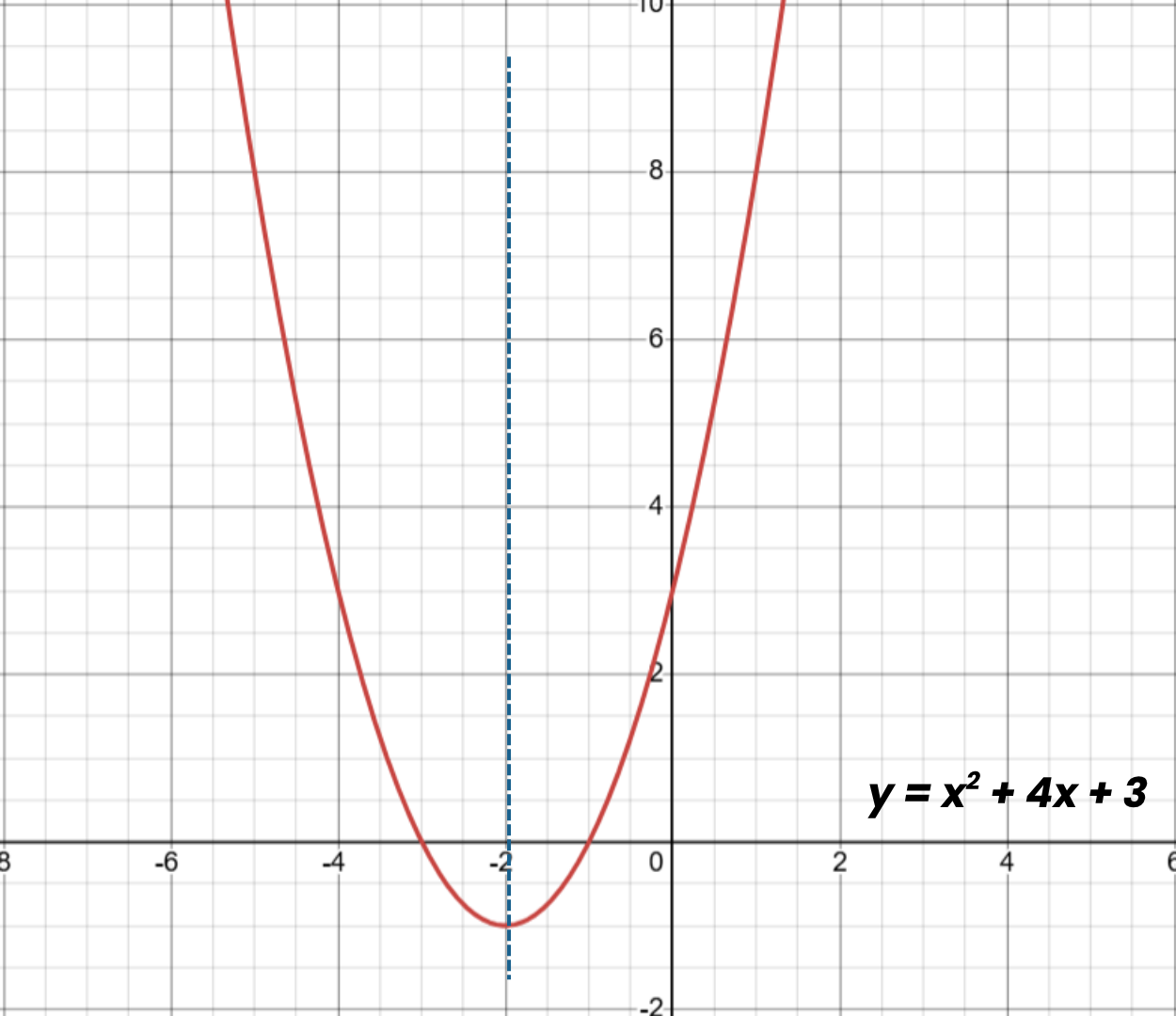
For example, the given quadratic function in standard form is y = x² + 4x + 3.

‍

In this equation, the coefficients are: a = 1 , b = 4 , c = 3

‍

2. Plug the values of a and b into the formula x=-b/2a.

‍

x = - (4) / 2(1)

x = -4 / 2

x = -2

‍

3. The result is the x-value of the axis of symmetry.

‍

Therefore, x = –2 is the axis of symmetry of the parabola, indicating that the vertical line of symmetry passes through that point on the graph.

‍

‍

‍

Example 1:

‍

Find the axis of symmetry of the quadratic equation y = x² - 6x + 5.

‍

Solution:

‍

a = 1 , b = -6 , c = 5

‍

Substituting the given values into the axis of symmetry formula:

‍

x = - (-6) / 2(1)
x = 6 / 2
x = 3

‍

Therefore, the axis of symmetry is x = 3. 

‍

Example 2:

‍

Find the axis of symmetry of the graph y = 3x² - 12x + 5.

‍

Solution:

‍

a = 3 , b = -12 , c = 5

‍

Substituting the given values into the axis of symmetry formula:

‍

x = - (-12) / 2(3)

x = 12 / 6

x = 2

‍

Therefore, the axis of symmetry is x = 2.

‍

‍

Find the Axis of Symmetry of a Parabola in Vertex Form

‍

When a quadratic function is written in vertex form,  y = a (x - h)²  + k, the values of h and k represent the coordinates of the vertex.

‍

To find the axis of symmetry, we simply use the formula: x = h. 

‍

1. Identify the coefficients from the given equation.

‍

For example, the given equation in vertex form is y = 2 (x - 3)² + 5.

‍

In this quadratic function, the coefficients are: a = 2 , h = 3 , k = 5‍

‍

2. Determine the vertex (h, k).

‍

Based on the data above, the vertex of the parabola is (3, 5).‍

‍

3. The value of h is the axis of symmetry.

Therefore, x = 3 is the axis of symmetry of the parabola, indicating that the vertical line of symmetry passes through that point on the graph.

‍

‍

Example 3:

‍

Find the axis of symmetry of the parabola y = 3 (x - 2)² - 4.

‍

Solution:

‍

a = 3, h = 2, k = -4

‍

Substituting the given values, the vertex coordinates are (2, -4).

‍

Since the axis of symmetry always passes through the vertex, the value of h gives us the line of symmetry.

‍

Thus, the axis of symmetry is x = 2.

‍

‍