Radius of a Circle - Properties and Formulas

‍

The radius is a key element in understanding circle theorems. It represents the distance from the center of the circle to any point on its circumference. This simple measurement plays a crucial role in calculating both the area and circumference of a circle. A solid understanding of the radius and how it relates to other parts of a circle is essential for solving problems in geometry and has practical applications in fields like engineering, design, and architecture.

‍

In this lesson, you’ll learn:

• What is a radius

• The main parts of a circle'

• The standard equation of a circle

• Formulas to find the radius of a circle

‍

What is a Radius?

‍

A circle is a round, two-dimensional shape where every point on its edge is the same distance from the center. The line segment that connects the center to any point on the circumference is called the radius. No matter where it touches the edge, the length of the radius remains the same.

‍

The radius of a circle is half the length of the diameter and is commonly represented by 'r'‍ in circle-related geometric formulas. Moreover, it is an important dimension in three-dimensional shapes like spheres, hemispheres, and cones or cylinders with circular bases. That’s why learning how to find the radius is a key skill in mathematical problem-solving.

‍

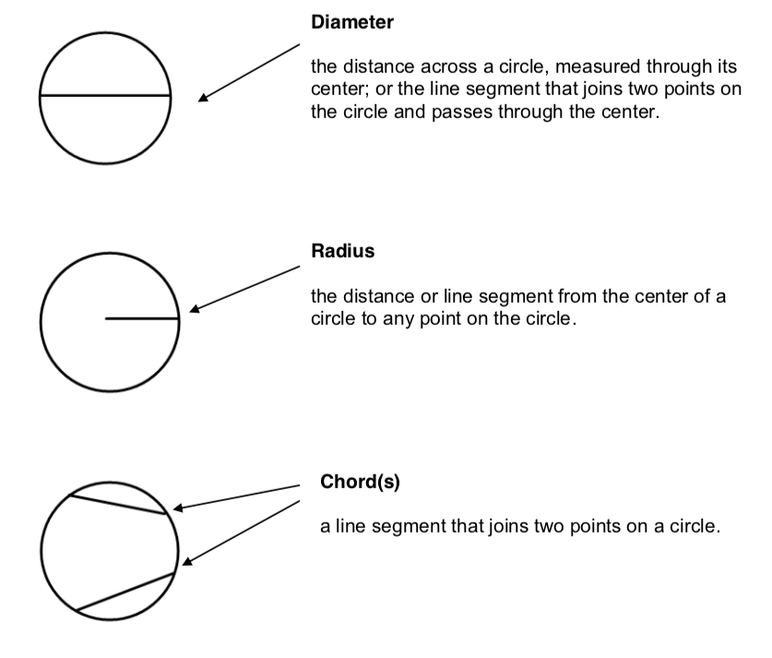
Main Parts of a Circle

‍

Before we delve deeper into the radius of the circle, let’s familiarize the different parts of the circle:

‍

Center - The central point of the circle from which all points are equidistant.

‍

Radius - The radius of a circle is the distance from the center of the circle to any point on its circumference.

‍

Chord - The chord of a circle is a line segment that connects two points of the circle’s edge. A diameter is a special type of chord that passes through the central point.

‍

Diameter - The diameter of the circle is the straight line passing through the center and connects two points of the circle’s edge. (d = 2r)

‍

Circumference - The circumference of a circle is the distance around the boundary of the circle. (C = 2𝛱r)

‍

‍

Equation of a Circle

‍

The standard equation of a circle is given by:

‍

(x - h)² + (y - k)² = r² , where (h,k) represents the center of a circle.

‍

For example, the equation of the circle is (x - 3)² + (y - 2)² = 25.

‍

In this case, the circle’s center is at (3,2) and the radius is the √25, which is 5.

‍

Radius of Circle Formulas

‍

The radius of a circle can be calculated using different formulas depending on the given parameters. Let’s explore each method below.

‍

Find the Radius from the Diameter

‍

The diameter of a circle is twice the length of the radius. This relationship is written as d = 2r.

‍

To find the radius when the diameter is known, simply divide the diameter by 2.

‍

Example: A circle has a diameter of 12 inches. What is the radius?

‍

r = d / 2

r = 12 / 2

r = 6 inches

‍

The radius of the circle is 6 inches.

‍

Find the Radius from the Circumference

‍

The circumference of a circle is expressed by the mathematical formula C = 2𝛱r.

‍

To find the radius when the circumference is given, simply divide the circumference by 2𝛱.

‍

Example: A circle has a circumference of 21 inches. What is the radius?

‍

r = C / 2𝛱

r = 21 / 2(3.14)

r = 21 / 6.28

r = ≈ 3.34 inches

‍

The radius of the circle is approximately 3.34 inches.

‍

Find the Radius using the Area

‍

The area of a circle is the total space enclosed within its boundary. It is calculated using the formula A = 𝛱r²_.

‍

To find the radius when the area is given, rearrange the formula to r = √A/𝛱.

‍

Example: A circle has an area of 254 square inches. What is the radius?

‍

r = √A / 𝛱

r = √(254) / (3.14)

r = √80.89

r = 8.99 or ≈ 9 inches

‍

The radius of the circle is approximately 9 inches.

‍

Find the Radius from a Chord

‍

A chord s a line segment that connects two points on the circumference of a circle. When a line is drawn from the center of the circle perpendicular to a chord, it bisects the chord into two equal parts.

‍

This forms a right triangle where:

The radius is the hypotenuse
Half of the chord is the base
The perpendicular line from the center to the chord is the height

‍

Using the Pythagorean Theorem, we can find the radius of the circle.

‍

Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

‍

Based on this principle, we can use the formula r² = (c/2)² + d²to find the radius.

‍

where:

r = radius (hypotenuse)

c = length of the chord

d = perpendicular distance

Example: The length of the chord of a circle is 12 cm, and the perpendicular distance from the center to the chord is 5 cm. Find the radius of the circle.

‍

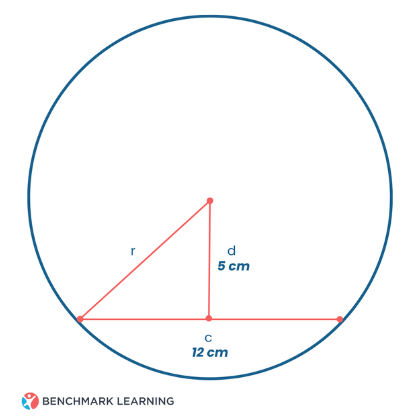
Given:
‍c = 12 cm d = 5 cm

‍

Solution:

r² = (12/2)² + 5²

r² = 6² + 5²

r² = 36 + 25

r = √61

r = 7.81 cm

‍

The radius of the circle is approximately 7.81 cm.

‍

Key Takeaway

‍

The radius is a fundamental part of a circle, measuring the distance from the center to any point on its edge. It plays a crucial role in solving problems related to area, circumference, and other geometric properties of circular shapes.

‍

To determine the radius, we can use various formulas depending on the parameters given. Mastering how to find and apply the radius deepens your understanding of circles and strengthens your ability to solve more complex problems involving spheres, hemispheres, and other 3D shapes with circular bases.